- Författare admin carl@lifeloveeveryday.com.
- Public 2023-12-16 19:28.
- Senast ändrad 2025-06-01 06:13.

Exempel på det gyllene snittet kan hittas överallt i klassisk arkitektur, konstverk, natur och till och med musik. Detta uttryck för proportioner, även känt som det gudomliga förhållandet, erbjuder harmonisk komposition genom tillämpning av ett irrationellt tal (1,618) i design, både naturligt och mänskligt skapat. Troligtvis är du omedveten om matematiken bakom skönheten i det gyllene snittet eftersom det producerar föremål och musik som du naturligtvis kommer att finna tilltalande utan att behöva någon förklaring.
Golden Ratio in Architecture
Det gyllene snittet skapar nästan perfekt skönhet i naturen och konsten. När du börjar leta efter exempel på det gyllene snittet i vardagen kan du bli förvånad över de många tillfällen det har använts för att skapa många monumentala byggnader och strukturer. När det gyllene snittet används i arkitektur sägs byggnaden vara skapad genom att använda "helig arkitektur". Genom att tillämpa beräkningen av det gyllene snittet på en kvadrat kan arkitekter och designers skapa den gyllene rektangeln, som tros ha de mest estetiskt tilltalande proportionerna för det mänskliga ögat.
Gyllene rektangelexempel: Parthenon

Phidias, den grekiske skulptören, använde det gyllene snittet i sitt arbete, speciellt när han började arbeta med banden han skulpterade precis ovanför Parthenonkolonnerna. Det är också viktigt att notera att det numeriska värdet som tilldelats det gyllene snittet, Phi, namngavs till hans ära.
Om du mäter måtten på Parthenons exteriör kommer du att upptäcka att den inte bara bildar en gyllene rektangel, utan att det också finns många gyllene rektanglar mellan kolumnerna. Denna heliga struktur är ett vackert exempel på det gyllene snittet i arkitektur.
Gyllene triangeln Exempel: Den stora pyramiden i Giza
Det gyllene snittet, den gyllene rektangeln och den gyllene triangeln kan alla hittas i perfektionen av ett av världens sju underverk, den stora pyramiden i Giza. För att hitta det gyllene snittet måste du halvera den kvadratiska basen av pyramiden och dra en vertikal linje upp i mitten av pyramiden. När denna är kopplad till en vinklad sida av pyramiden kan du enkelt se hur den bildar Gyllene Triangeln med ett förhållande på 1,618, Gyllene Snittet.
Andra arkitektoniska exempel
Du kan hitta många exempel på antik till modern helig arkitektur och byggnader med Gyllene snittet.
- Chartres Cathedral - Centre, Frankrike
- Notre Dame - Paris, Frankrike
- Porch of Maidens - Akropolis, Aten
- Taj Mahal - Agra, Indien
- United Nations Building - New York, New York
Gyllene snittet i konstexempel
Du kan hitta många exempel av målare som använde det gyllene snittet. Dessa perfektionsverk skapades genom att använda förhållandet mellan gyllene rektanglar och gyllene trianglar. Konst skapad baserad på den gyllene rektangeln visar sig vara mer tilltalande för det mänskliga ögat. Det är ett av mysterierna som omger denna perfekta rektangel och det gyllene snittet.
Golden Ratio in Art

Konstexempel med gyllene snitt inkluderar:
- Leonardo Di Vinci - Mona Lisa, Vitruvian Man
- Botticelli - Venus födelse
- Michelangelo - Heliga familjen, 'David'
- Raphael - Crucifixion
- Rembrandt - Självporträtt
- Salvador Dali - Nattvardens sakrament, minnets uthållighet
Using Golden Ratio i konstkomposition
Inom en gyllene rektangel finns vissa områden som visar sig vara mer visuellt tilltalande än andra områden. Dessa punkter upptäcks genom att dra en linje från det nedre hörnet av rektangeln till det motsatta hörnet och upprepa den med det andra nedre hörnet. Dessa linjer kommer att skära varandra i den exakta mitten av den gyllene rektangeln. Mät sedan halvvägs längs varje linje med början från mittpunkten. Dessa fyra punkter kallas rektangelns ögon (Golden Ratio). Målningens huvudsakliga brännpunkt ritas eller målas sedan inom dessa intressepunkter (förhållanden).
Golden Ratio in Music

Musik är sammansatt av numeriskt värde och när det gyllene snittet används för att skapa ett musikstycke blir det ett levande exempel på matematik. Fibonacci-sekvensen är också utbredd i musik:
- Det finns åtta toner i en skala.
- Tredje- och kvinttonen är grunden för ackord.
- Längden, eller oktav, av en ton är 13 toner.
Sekvenseringen fortsätter genom ett musikstycke och blir mer komplex när det når det gyllene snittet.
Kompositörer som använde det gyllene snittet
Några av de mest kända klassiska kompositörerna använde Golden Ratio och Fibonacci Sequencing i sina musikstycken, inklusive Bach, Beethoven, Chopin och Mozart. Vissa moderna kompositörer som Casey Mongoven har utforskat det gyllene snittet i sin musik.
Golden Ratio Exempel i naturen

Var finns det gyllene snittet i naturen? Det är i Golden eller Fibonacci Spiral, som kan skapas genom att använda Golden Ratio. Detta är ett fenomen som finns mycket i den naturliga världen. En växts blad växer så att så många som möjligt kan spiral upp i stjälken. Ett nytt blad bildas först efter att det som fortsätter att det har bildats.
- Spiralkaktus
- Spiralgalaxer
- Solrosor
Blommor med Fibonacci-sekvensen
Vissa blommor har blomblad som följer Fibonacci-sekvensen:
- Tre kronblad:Iris, lilja, orkidéer, trillium
- Fem kronblad: Smörblommor, pelargoner, hibiskus, morning glory, nasturtium
- Åtta kronblad: Delphiniums
- 13 kronblad: Vissa varianter av prästkragar, raggwort, ringblomma
Fibonacci-spiral i tallkottar

Beroende på trädslag kan du också se det gyllene snittet i arbete inom en Fibonacci-nummerserie i tallkottar. Du kan hitta en serie av åtta spiraler på ena sidan av tallkotten, med 13 spiraler på den andra. Ett annat kottemönster har fem spiraler på ena sidan med åtta på den andra.
Golden Ratio in Humans
Detta förhållande är också viktigt för inte bara hur människor ser på varandra utan också för hur deras kroppar fungerar och i deras DNA.
DNA avslöjar det gyllene snittet
Ett av de mest fantastiska exemplen på Golden Ratio finns i den mänskliga DNA-strukturen. Detta kan ses i ett enskilt DNA-tvärsnitt som avslöjar att DNA-dubbelhelixen bildar en dekagonform. Detta är en kombination av två femhörningar, roterade 36 grader från varandra, bildar DNA-dubbelhelixen. Den dubbla helixspiralen bildar själv en femhörning. Till och med en enda DNA-molekyl avslöjar en grund för det gyllene snittet eller den gudomliga proportionen.
Matematiken bakom det gyllene snittet
Att hitta det gyllene snittet i verkligheten är enkelt, eftersom det ser ut runt omkring dig. Det är en matematisk truism som används för att definiera vad som allmänt är känt som det perfekta numret som finns i naturen och som har duplicerats och imiterats av människor i århundraden. Den förenklade skönheten i detta nummer döljer dess komplexitet i utförandet. För att förstå teorin bakom det gyllene snittet måste du först utforska Fibonacci-sekvensen av förhållandet.
Fibonacci-sekvensen och det gyllene snittet
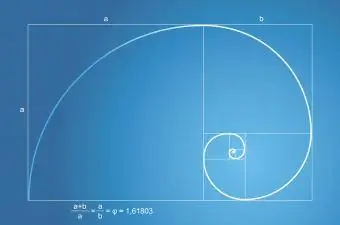
Fibonacci-sekvensen eller -serien har ett förhållande till det gyllene snittet. Fibonacci-serien visar sig i antalet blad på en växt och antalet kronblad på en blomma. Fibonacci-spiralen, som finns i naturen, är alltid en del av en gyllene rektangel med ett gyllene snitt.
Fibonacci-seriens matematik är enkel:
- Sekvensen börjar med 0 och 1.
- Lägg bara till de två sista siffrorna för att få nästa nummer i serien.
- 0+1=1, 1+1=2, 1+2=3, 2+3=5, 3+5=8, och så vidare.
- Det här Fibonacci-seriens exempel blir: 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 och så vidare.
Fibonaccis förhållande till det gyllene snittet förverkligas när det läggs framåt, längre och längre. Ju mer du lägger till serien, desto närmare kommer du det gyllene snittet.
Skapa en gyllene rektangel och triangel
För att skapa en gyllene rektangel med Fibonacci-sekvensen börjar du med en kvadrat. Du kommer att börja bygga en rektangel genom att lägga till ytterligare en kvadrat till den ursprungliga kvadraten. Kom ihåg att använda formeln: 0+1=1 är den första kvadraten, 1+1=2 - du lägger till ytterligare en kvadrat.1+2=3 lägger du till tre rutor och sedan, 2+3=5, lägger du till fem rutor. Du kommer att fortsätta att lägga till rutor och så småningom bilda en gyllene rektangel.
En gyllene triangel kan skapas genom att dela en gyllene rektangel från ett hörn till det motsatta hörnet. Detta skapar en triangel där dess tre sidor eller vinklar har en proportion på 2:2:1, vilket betyder att de två långsidorna är lika långa och den korta vinkeln är exakt hälften av längden av de två längre.
Golden Ratio in the Real World
Det gyllene snittet kallas ofta för det gudomliga förhållandet på grund av dess framträdande plats i naturen och i mänskliga kroppar. Upptäckten att det gyllene snittet finns i så många levande varelser skapade en vördnad för denna magiska proportion, och den fortsätter att vara en inspiration för artister och kreatörer idag.